Building an Object-Oriented Parasitic Metalanguage
It’s all about pattern matching. The rest is just details.
My last post on OMeta# focused on what it is and the vision I have for its future. Briefly, OMeta is a new language that makes it easier to design programming languages in an object-oriented fashion using very few lines of quite readable code. OMeta# is my attempt to support OMeta on the .NET runtime. My main strategy has been to base its design off of Alessandro Warth’s JavaScript implementation of OMeta/JS. This post gets into the specifics of how I’ve done this so far, but my hope is that you might see some places where the design could use improvement and that you might be encouraged to leave a comment so that it could get better.
High Level Design
At its core, OMeta has a very simple design. The highest level of abstraction is a grammar. Here is a calculator grammar in the current implementation of OMeta#:
ometa Calculator <: Parser {
Digit = Super((Digit)):d -> { d.ToDigit() },
Number = Number:n Digit:d -> { n.As<int>() * 10 + d.As<int>() }
Digit,
AddExpr = AddExpr:x '+' MulExpr:y -> { x.As<int>() + y.As<int>() }
AddExpr:x '-' MulExpr:y -> { x.As<int>() - y.As<int>() }
MulExpr,
MulExpr = MulExpr:x '*' PrimExpr:y -> { x.As<int>() * y.As<int>() }
MulExpr:x '/' PrimExpr:y -> { x.As<int>() / y.As<int>() }
PrimExpr,
PrimExpr = '(' Expr:x ')' -> { x }
Number,
Expr = AddExpr
}
A grammar is composed of rules (which are sometimes referred to as “productions”). Both the grammar itself and the rules have the same form:

Going into the rule is a list of things of the input type (here they’re represented by red circles) and coming out on the right is a list of things of the destination type (represented by purple triangles). As you can see from the diagram, the output list can have lists inside of it. In the calculator grammar, the circles are individual characters and the output is a single integer.
My “Ad Hoc, Informally-Specified, Bug-Ridden, Slow Implementation of Half of Common Lisp”
As an implementer of OMeta, you have to make several design choices. One of the first is how to represent grammars. Since OMeta is object-oriented, I decided that it made sense to represent grammars as a .NET class (a.k.a. “Type”). Grammars contain rules; the obvious choice for implementing rules is to use a method. This especially makes sense because rules can refer to rules in their base grammar. For example, the above calculator grammar has a rule called “Digit” which captures a single numeric digit. The “Digit” rule applies the “Digit” rule in its base grammar (Parser) that simply captures a digit character. It does this by applying the special “Super” rule which will use the base grammar to apply the rule that is specified by an argument. Since rules are implemented as methods and rules can “override” their definition from their base grammar, it made sense to make rule methods “virtual.”
Another important decision is how to represent data going into and out of a rule application. An easy choice is to represent the data in a List<T>. This works out well except for the small detail that lists can contain other lists. This nested list idea has been around for at least 50 years in LISP and languages derived from it (like Scheme). Since it has worked out fairly well in those languages, I stole the idea of a LISP-like list in my OMetaList<TInput> class which is a list of other lists with a special case that makes lists of length 1 equivalent to the element itself.
These decisions get us started, but a problem comes up if you try to implement the factorial function using recursion in an OMeta grammar:
ometa Factorial {
Fact 0 -> { 1 },
Fact :n ?(n.As<int>() > 0) Fact((n.As<int>() - 1)):m -> { n.As<int>() * m.As<int>() }
}
If you look carefully at this grammar, you’ll see that it only says two things:
- If the next element of input matches a 0, return 1
- If the next element of input is something greater than zero, store its value to “n” and then apply the “Fact” rule supplying it with the value of “n - 1” and capture that result to “m”. Finally, return “n * m”.
What might not be obvious at first is that any time you store something to a variable using an expression like “:n”, the value stored must be of the destination type (e.g. a triangle in the diagram). This makes us need to update our mental model for how OMeta works. We need a place to store rule “arguments” which are already in the destination type.
One way of doing this is to create an argument stack that is separate from the rest of the input. Additionally, we’ll need a place to store grammar-local variables as well as a place to remember previous results of rule applications for performance reasons. This gives us a much more complete picture of what really occurs:
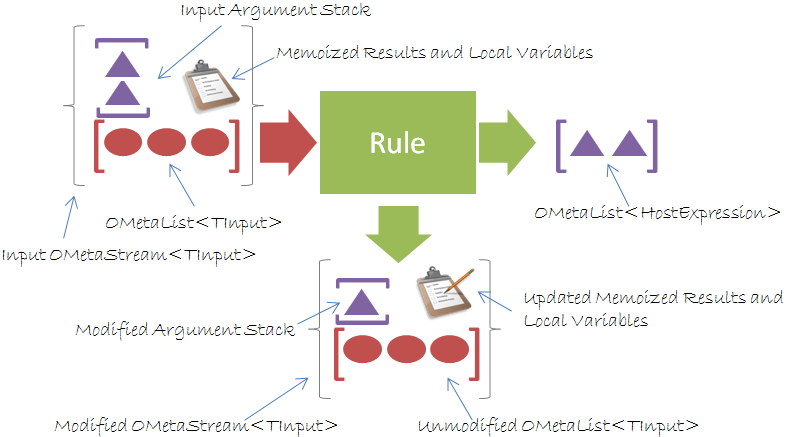
When a rule needs to consume input, it will first attempt to grab pop an item from the argument stack. If the stack is empty, then next element from the input list can be read.
I decided to store all of these details into a single class which I call an OMetaStream<TInput> which internally uses an OMetaList<TInput> for input data and an OMetaList<HostExpression> for storing the argument stack. The arguments are actually stored in an OMetaProxyStream<TInput> which inherits from OMetaStream<TInput>, but this is just an implementation detail.
With the major data structures out of the way, one important choice remaining is how to handle going down the wrong path. If you look at the calculator grammar, you’ll see that the “AddExpr” rule can be of the form “x + y”, or “x - y”, or a “MulExpr”.
How does OMeta know which one to take? It makes a prioritized choice by trying each of the alternatives in the order specified. If it discovers that it has gone down the wrong path (e.g. the next item from the input is a “-“ instead of a “+”), it needs to backtrack and reset itself to the condition it was in before the bad choice and then try the next option.
There are two obvious ways of doing this. The first approach is to leverage runtime support by using exceptions. This is exactly what OMeta/JS does. Using exceptions has an advantage of making the generated code simpler because there is no explicit code to “unwind the stack” in case you go down a bad path.
Although it makes the code easier to read, I decided against using exceptions and instead chose to use methods that return a boolean value to indicate if they succeeded. I did this for two important reasons:
- .NET does a bit of extra work when an exception is thrown (e.g. getting a stack trace). Therefore, throwing an exception has a non-trivial performance penalty.
- Rules have prioritized choice. This means that failing a single choice doesn’t imply that the whole rule fails. Failing can be a very common occurrence (it’s not exceptional) and this makes it very performance sensitive.
Here’s a small glimpse of what the generated code looks like for attempting to apply the “AddExpr” rule:
OMetaList<HostExpression> x;
OMetaStream<char> addExprOut;
if(!MetaRules.Apply(AddExpr, inputStream2, out x, out addExprOut))
{
return MetaRules.Fail(out result2, out modifiedStream2);
}
In this case, AddExpr is the name of the rule which is implemented as a method. Data is read from the “inputStream2” which is an OMetaStream (where the red circles are characters). The resulting list is saved to the “x” variable and the modified stream is stored in “addExprOut”. In order to make back-tracking easier, OMetaStreams are mostly immutable, which means that they can’t change. Instead of updating the stream itself, you get a fresh copy of the stream that contains what the result would be. If you need to back track, you can simply ignore the rule application output. As a side benefit, it makes it slightly easier to debug since you don’t have to worry about the mutations that could otherwise occur.
Parasitic?
 OMeta’s creator likes to refer to OMeta as a “parasitic language” because it doesn’t exist on its own. It always lives on top of a “host language.” This makes an implementation usually defined in terms of its host language. That’s why there is “OMeta/JS” which uses JavaScript as a host language. Although my ultimate goal for OMeta# is to have the host language be any .NET language, I decided to use C# as my first host language.
OMeta’s creator likes to refer to OMeta as a “parasitic language” because it doesn’t exist on its own. It always lives on top of a “host language.” This makes an implementation usually defined in terms of its host language. That’s why there is “OMeta/JS” which uses JavaScript as a host language. Although my ultimate goal for OMeta# is to have the host language be any .NET language, I decided to use C# as my first host language.
One of the first issues that came up was trying to recognize what exactly is C# code. As you can see from examples in my last post, my first attempt was to pick a really ugly pattern that wouldn’t occur in normal use. I picked two consecutive @ signs as in:
@@/*This is C#*/@@It worked out well, but it had the downside that it was, well… incredibly ugly. I have since written a rudimentary C# recognizer written in OMeta# itself that is aware of strings and comments. The upside is that the syntax looks a little nicer:
{ /*This is C#*/ }Using C# as the host language had several implications. The most challenging was working with C#’s static type system. This was both a blessing and a curse. On the one hand, I had to constantly think about where the data came from and where it was going. This forced me to actually understand the overall design better. On the other hand, I had to spend so much time thinking about it. Late-bound systems with dynamic typing such as Smalltalk and JavaScript remove the need for people to spend so much time doing this.
I’m optimistic that over time a lot of the stronger annoyances will go away. For example, the current syntax forces type identification as in:
-> { n.As<int>() * 10 + d.As<int>() }
Where, OMeta/JS can just say:
-> { n * 10 + d }
I’m not exactly sure how to do this yet. My initial guess is that I might be able to write some sort of type inference algorithm (preferably written in OMeta#) that could do a reasonable job. My current ideas are tied too closely with the specific host language and would require a bit of work to port them to other host languages like Visual Basic. Another approach is to implement one or more helper classes that could enable duck typing (e.g. if it looks like a certain type, walks like that type, and quacks like the type, it’s probably that type).
Being able to have strong static typing internally while having a very clean syntax would be ideal (e.g. sort of like the C# 3.0 “var” keyword). Static typing is usually harder to achieve, but if you can do it well, you get many benefits. C# designer Anders Hejlsberg said it well in a recent interview:
“I don’t see a lot of downsides to static typing other than the fact that it may not be practical to put in place, and it is harder to put in place and therefore takes longer for us to get there with static typing, but once you do have static typing. I mean, gosh, you know, like hey – the compiler is going to report the errors before the space shuttle flies instead of whilst it’s flying, that’s a good thing!”
Another issue that came up was properly handling inheritance. It makes sense to use “virtual” methods for rules, but this also requires you to emit the “override” directive to avoid warnings. Another warning cropped up from my use of the “base” keyword in the many delegates that makes it convenient from a code emission perspective, but frustrating from a verifiable security perspective. Both of these warning are being left for a latter phase.
Compiler issues were only one factor. The other significant piece was aesthetics. A notable number of rules yield specific lists as their result. C# doesn’t quite have a good, clean way of expressing an OMetaList (that is, a list of lists). In order to get around this, I created the “Sugar” helper class which makes it slightly easier to write these lists. It’s still far from perfect. Instead of having a nice way for expressing lists like that OMeta/JS:
-> ['add', x, y]
You have to do this instead:
-> { Sugar.Cons("add", x, y) }
This annoyance can probably be fixed by tricking the C# recognizer to act as if C# had a nice implicit way of expressing an OMetaList and then re-writing the expression to use the Sugar class.
Beyond C#, there is the “meta” “host language” which is the .NET common language runtime itself. For code to play nice on it, it should abide by the .NET framework design guidelines which dictate naming conventions and general practices. This had a parasitic effect in that it led me to name my rules after the naming guidelines for methods (e.g. they must be PascalCased). Thus, in OMeta# there is the “Digit” rule instead of the “digit” rule. OMeta/JS opts to prefix metarule method names with an underscore to make them not collide with other rules. I also wanted to hide metarules so that people would have to try harder to do the wrong thing; the best I could come up with to convey this idea was to implement them using an explicit interface exposed via a property (e.g. instead of “_apply”, I have “MetaRules.Apply”).
Being a Contextual Packrat
The last intriguing thing about OMeta is exactly how it implements parsing. It uses a technique called a Parsing Expression Grammar (PEG) that Bryan Ford introduced in 2004. It’s just a fancy way to say you support the following features: (The table comes from the OMeta paper. I’ve also included how OMeta# implements them to prove its legitimacy):
| expression | meaning | OMeta# Function |
| e1 e2 | sequencing | Seq |
| e1 e2 | prioritized choice | MetaRules.Or |
| e* | zero or more repetitions | MetaRules.Many |
| e+ | one or more repetitions (not essential) | MetaRules.Many1 |
| ~e | negation | MetaRules.Not |
| <p> | production application | MetaRules.Apply |
| 'x' | matches the character x | Exactly |
The most interesting aspect to me is the prioritized choice. This is in contrast to “Context-Free Grammars” (CFGs) which are the traditional way of defining parsers. To highlight the difference, consider parsing this line of C/C++ code:
if (condition1) if (condition2) Statement1(); else Statement2();Is it the same as:
if (condition1) { if (condition2) { Statement1(); } else { Statement2(); } }… or is it:
if (condition1) { if (condition2) { Statement1(); } } else { Statement2(); }This is the classic “dangling else” problem. Context Free Grammars usually have this problem because they are free of any context when they are parsing (surprise!). In these situations, you often have to rely on something besides the grammar itself to resolve these ambiguities. Parsing Expression Grammars don’t have this type of problem because you specify explicitly which one to try first. The prioritized choice therefore avoids ambiguity.
In order to make the performance relatively in line with the size of the input, a technique of “memoization” is used. This means the parser remembers what it has done previously; it does this as a space-time tradeoff. Keeping all those previous values have given them the reputation of being a “packrat” parser.
Let’s say you have
AddExpr = AddExpr:x '+' MulExpr:y -> { x.As<int>() + y.As<int>() }
AddExpr:x '-' MulExpr:y -> { x.As<int>() - y.As<int>() }
MulExpr
and you try the first choice (AddExpr:x ‘+’ MulExpr:y), but you get to where you’re expecting a “+” and it isn’t there. You’ll notice that the second choice (AddExpr:x ’-‘ MulExpr:y) repeats the first part (namely AddExpr:x). Instead of re-evaluating it, you can just retrieve the stored value that you remembered, or rather memoized.
Well, it’s almost that simple. Note that the definition of an add expression (AddExpr) is left-recursive. This means that the left side is defined in terms of itself. A naïve implementation of the parser would try to evaluate “AddExpr” by applying the first choice which started with a AddExpr which would then cause it to try to apply AddExpr again and eventually cause a stack overflow.
It’s not a trivial problem to fix. In fact, the paper that introduced Parsing Expression Grammars said that left-recursion should be avoided since you can rewrite the rule to avoid left-recursion. This is unfortunate guidance because the rewritten rule sometimes loses the clarity that the left-recursive version of the rule had.
At the start of this year, a paper came out showing a very clever trick that makes left recursion possible.
Say that we’re parsing the expression “1+2+3” using the “AddExpr.” At the start of the expression we look at our memoization table to see if we have a precomputed value for “AddExpr”. Since it is our first time, we won’t find anything. The first part of the trick is to immediately store the result of “Fail” as the memoized result for AddExpr when starting at offset 0. We do this before we attempt to apply the rule.
When the parser uses recursion and finds itself again asking for the value of “AddExpr” at position 0, it will find a result of “fail” and thus fail that choice. It will then continue down to “MulExpr” where it will eventually match “1”. The second part of the trick is to treat this value of “1” for “AddExpr” at position 0 as a “seed parse.” The parser will then attempt to “grow the seed” by starting over at the beginning of the input stream, but this time it will remember its previous successful match. This will cause it to match “1+2” for AddExpr and then start over again by growing the seed to finally match “1+2+3.”
In hindsight, it’s a very simple idea. However, I say that only after some serious debugging time where I kept finding problems in my poor implementation. Alas, the entire algorithm is implemented in only a few lines of code in the “MetaRules.Apply” function in OMetaBase.cs.
So there you have it, you now know all of the interesting ideas in OMeta#.
Where is This Going?
OMeta# is a hobby project that’s been a labor of love for me. You might have already guessed that if you noticed that most check-ins occur late at night or on the weekends. It’s been slow, but it’s coming together. Probably the most exciting highlight in the development came when I got enough of OMeta# working that I could rewrite parts of itself in OMeta#. This has the benefit of being cool from a meta self-reproducing level, but it’s also a bonus because the code becomes much more readable and introspective. For example, compare the C# recognizer that I wrote by hand to the OMeta# grammar version that implements the same idea.
This approach of writing more of OMeta# in OMeta# will continue. It’s my hope that as much as possible will be written in itself. A significant next step would be to rewrite the code generator as an OMeta# grammar. This isn’t a new design idea. Each subsequent version of Smalltalk has been bootstrapped by its previous version.
I’ll be the first to point out that there are a lot of rough edges to my current implementation. If you look around the source code, you’ll see several comments labeled “// HACK” where I admit a hacked version of an idea. One of the most glaring problems is that debugging is annoyingly difficult. I haven’t yet implemented an optimizer for the generated code which causes a lot of unnecessary metarule applications. The second annoyance is that just stepping into so many methods that fail often takes a long time. Over time, I hope to add better hints to get more traditional error messages that you get from good compilers so that you don’t have to step through the generated code to debug a grammar.
As mentioned earlier, the language recognizer could use some work to make the syntax cleaner as well inferring types so that grammar writers don’t have to explicitly declare them. I have confidence that the work that would go into a good C# host language implementation would directly port to other languages such as Visual Basic.
There’s also a great need cross pollination with other projects such as the Dynamic Language Runtime (DLR) which has already tackled some of the issues that OMeta# will face. Additionally, languages such as F# have similar data structures already built-in that OMeta uses. Boo and Nemerle have interesting extensibility points which could provide some good ideas. The problem for me is that there is so many different places to look. It’d be great if you know these languages (or others) and could tell me via a comment or better yet, by sending code of how they could help OMeta#.
As of right now, I plan on keeping the core functionality in C# rather than rewriting everything in another language or by using the DLR. The main reason is that C# is wide-spread in availability, both on .NET as well as on Mono. A second reason is that I would like to keep the outside dependencies on OMeta# as small as possible.
OMeta is a beautiful in the same sense that mathematics can have a simple beauty. LISP has been referred to by some as “The Most Important Idea in Computer Science” largely because its core ideas could be expressed on a half page of the LISP 1.5 manual (page 13 to be exact). This elegance is similar to mathematics of Maxwell’s Equations describing electromagnetism.
It’s my hope that I won’t mess up the implementation to the point where this elegant beauty is lost. Currently it’s way too ugly. I see some of the rough edges, but I’m sure you can help me discover others along with how to fix them. If this post sounds too complicated, it’s not you, it’s me. Let me know if something doesn’t make sense and I’ll try to provide clarification.
If you’re interested in OMeta#, I highly encourage you to download the latest version of the source code from CodePlex and step through the unit test runner to see things get built up.
If you can, keep notes of all the places where you see me doing something and let me know about them either through comments or via email. In addition, I also highly recommend experimenting Alessandro Warth’s great OMeta/JS implementation via your web browser.
Happy OMeta-ing!